Antwort Wie viel Standardabweichung ist akzeptabel? Weitere Antworten – Welche Standardabweichung ist akzeptabel

Wenn zum Beispiel die Standardabweichung einer Messgröße 0,1 mm beträgt und ein Toleranzband von +/- 0,5 mm akzeptabel ist, bedeutet dies, dass etwa 68% der Messwerte innerhalb dieses Bereichs liegen werden.Eine Standardabweichung zeigt an, wie genau ein Mittelwert ist. Ist sie groß, ist er ungenau. Bei einer Normalverteilung liegen 68,26 % aller Werte maximal eine Standardabweichung vom arithmetischen Mittel entfernt.99 schreibt, Größen, die über eins werden können aber als 0.11 und 0.99 schreibt. Wenn das so ist, dann gilt, dass Standardabweichungen auch größer als 1 werden können.
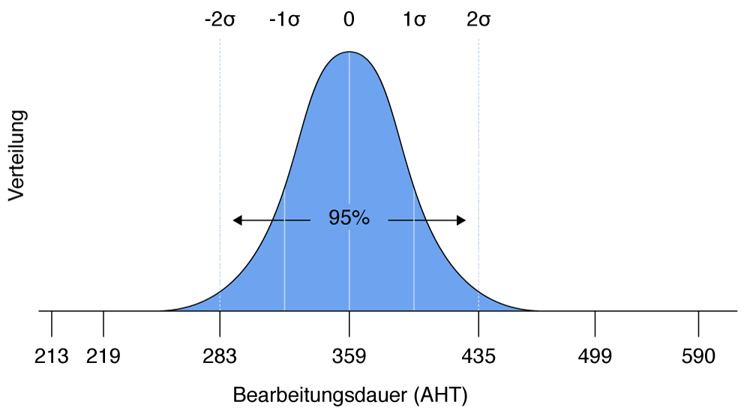
Warum muss die Standardabweichung größer 3 sein : Je größer die Standardabweichung eines Prozesses ist, desto mehr streuen die Daten um den Mittelwert. Damit wird die Glockenkurve breiter. Die Prozentanteile entsprechen der anteiligen Fläche unter der Kurve (Wahrscheinlichkeiten) bis zu den jeweiligen Anzahlen an Standardabweichungen.
Was ist eine normale Standardabweichung
Bei annähernd normal verteilten Daten liegen etwa 68% aller Daten innerhalb einer Standardabweichung vom Mittelwert. Etwa 95% liegen innerhalb von 2 Standardabweichung (genauer: 1,96) und 99,7% liegen innerhalb von 3 Standardabweichungen. Dies wird auch als 68-95-99,7 Regel bezeichnet.
Wann ist eine Standardabweichung signifikant : bei einem Wert von ≤ 1 % (2,3 Standardabweichungen) spricht man von einem sehr signifikanten und. bei einem Wert von ≤ 0,1 % (3,1 Standardabweichungen) spricht man von einem hoch signifikanten Ergebnis.
Wird die Standardabweichung kleiner, also s2 kleiner als s1, so wird die Kurve schmäler, wird die Standardabweichung größer, angenommen s3 größer s1, so wird die Kurve breiter. Die Standardabweichung s gibt also die Streuung, das heißt die Breite der Verteilung an.

In der Sigma-Umgebung um den Erwartungswert liegen 68,3 % der Ergebnisse. In der 2Sigma-Umgebung sind es 95,4 % und in der 3 Sigma-Umgebung 99,7 %.
Was ist eine geringe Standardabweichung
Die Standardabweichung ist ein sogenanntes Streuungsmaß aus der Statistik. Es gibt Auskunft darüber, wie weit die einzelnen Datenpunkte im Schnitt vom Erwartungswert entfernt sind. Eine niedrige Standardabweichung sagt aus, dass die Datenpunkte relativ nahe am Erwartungswert gelegen sind und vice versa.In der Regel wird ein Signifikanzniveau von 0,05 verwendet, was bedeutet, dass ein P-Wert kleiner als 0,05 als signifikant angesehen wird. Wenn der P-Wert größer als das Signifikanzniveau ist, wird die Nullhypothese nicht abgelehnt.90% der Werte von X liegen im Intervall [μ-1,64σ;μ+1,64σ]. 95% der Werte von X liegen im Intervall [μ-1,96σ;μ+1,96σ]. 99% der Werte von X liegen im Intervall [μ-2,58σ;μ+2,58σ].
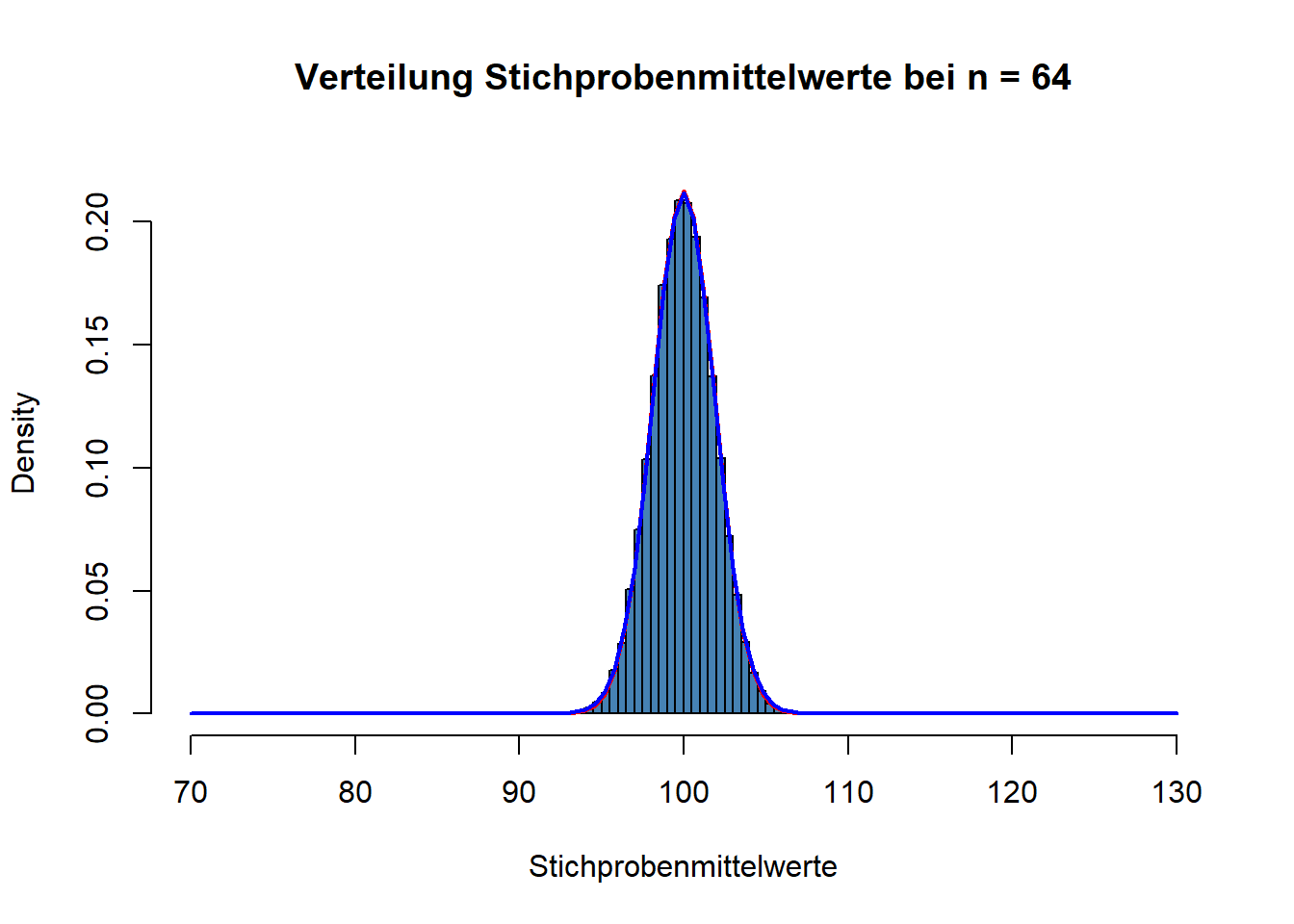
In der Sigma-Umgebung um den Erwartungswert liegen 68,3 % der Ergebnisse. In der 2Sigma-Umgebung sind es 95,4 % und in der 3 Sigma-Umgebung 99,7 %.
Welche Standardabweichung ist normal : Bei annähernd normal verteilten Daten liegen etwa 68% aller Daten innerhalb einer Standardabweichung vom Mittelwert. Etwa 95% liegen innerhalb von 2 Standardabweichung (genauer: 1,96) und 99,7% liegen innerhalb von 3 Standardabweichungen. Dies wird auch als 68-95-99,7 Regel bezeichnet.
Wann ist eine Abweichung signifikant : bei einem Wert von ≤ 1 % (2,3 Standardabweichungen) spricht man von einem sehr signifikanten und. bei einem Wert von ≤ 0,1 % (3,1 Standardabweichungen) spricht man von einem hoch signifikanten Ergebnis.
Was bedeutet 5% Signifikanzniveau
Signifikanzniveau einfach erklärt
Ein α-Niveau von α = 0,05 bedeutet, dass man eine Fehlerwahrscheinlichkeit von 5 Prozent in Kauf nimmt. Attestiert uns ein statistischer Test zum α-Niveau von 0,05 also Signifikanz, so liegen wir mit unseren Rückschlüssen mit einer Wahrscheinlichkeit von nur 5 Prozent falsch.
Sigma-Regeln Aufgaben mit Lösungen – Die Ein-Sigma-Regel
zwischen -21,55 Prozent und 41,29 Prozent.Standardabweichung als Zahlenwert immer berechnet werden. Im Gegenteil dazu kann die Interpretation der Varianz bzw. Standardabweichung als ein Maß der Streuung nur dann sinnvoll eingesetzt werden, wenn die Art der Verteilung bekannt ist.
Wie viel Prozent sind statistisch signifikant : Üblich sind Werte für das Signifikanzniveau von 5% oder 1%. Liegt die Fehlerwahrscheinlichkeit α darunter, dann ist das Ergebnis statistisch signifikant mit einer Wahrscheinlichkeit von 95% oder 99%. 1-β bezeichnet man als die Teststärke (statistical power) oder Sensitivität.



