Antwort Was besagt Normalverteilung? Weitere Antworten – Was sagt die Normalverteilung aus
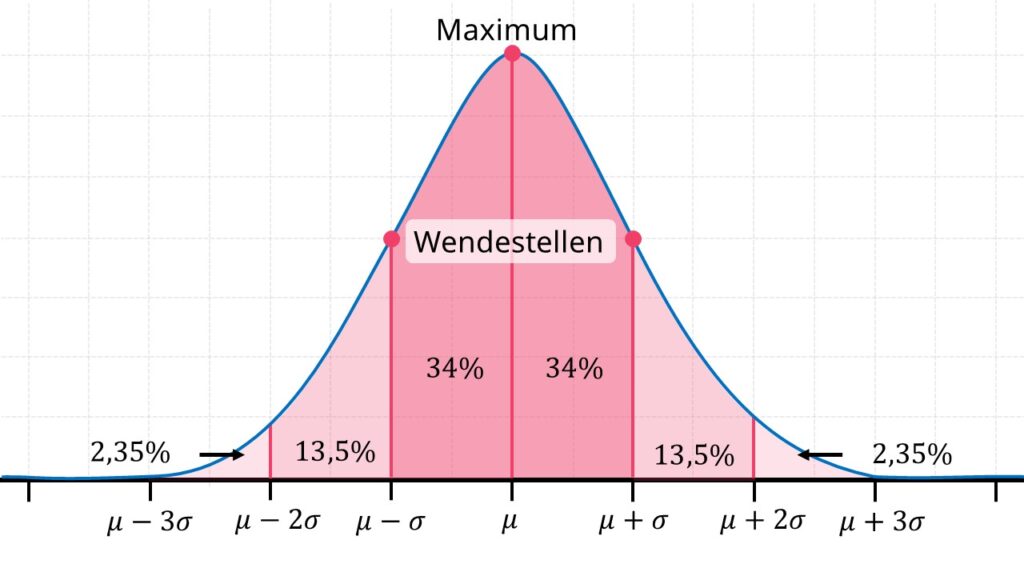
Die Normalverteilung wird verwendet, um Häufigkeiten von Daten und Beobachtungen darzustellen. Der Graph der Normalverteilung zeigt die Verteilung der Daten um den Mittelwert.Die 68-95-99.7 Regel besagt nun, dass: 68 % aller Männer zwischen 160 cm und 180 cm groß sind. 95 % aller Männer zwischen 150 cm und 190 cm groß sind. 99,7 % aller Männer zwischen 140 cm und 200 cm groß sind.Außerdem wissen Sie noch, dass das Gewicht normalverteilt ist. Konkret wissen Sie, dass das durchschnittliche Gewicht 80kg und die Streuung, die Standardabweichung, 3kg beträgt. Wenn Sie das alles wissen, dann können Sie die Verteilung des Gewichts auch grafisch veranschaulichen und erhalten nachfolgendes Bild.
Was bedeutet die Fläche unter der Normalverteilung : – Die Normalverteilung ist stets symmetrisch mit einer Symmetrieachse bei x = µ. – Die Fläche bzw. das Integral unter der Kurve von – ∞ bis + ∞ ist stets 1. Dies bedeutet, dass die Wahrscheinlichkeit aller Ausprägungen dieser Verteilung in Summe 1, also 100%, ist.
Warum Normalverteilung wichtig
Die besondere Bedeutung der Normalverteilung beruht unter anderem auf dem zentralen Grenzwertsatz, dem zufolge Verteilungen, die durch additive Überlagerung einer großen Zahl von unabhängigen Einflüssen entstehen, unter schwachen Voraussetzungen annähernd normalverteilt sind.
Wie prüft man auf Normalverteilung : Um deine Daten analytisch (mit statistischen Tests) auf Normalverteilung zu prüfen, gibt es verschiedene Test verfahren, die bekanntesten sind der Kolmogorov-Smirnov Test, der Shapiro- Wilk Test und der Anderson Darling Test. Mit all diesen Tests prüfst du die Nullhypothese, dass deine Daten normalverteilt sind.
Bei einer Normalverteilung liegen exakt 68,3 % der Daten in dem Bereich des Erwartungwerts +/-einer Standardabweichung (in unserem Beispiel also zwischen 170 cm und 190 cm. Etwa 95,5 % der Daten liegen im Bereich Erwartungswert +/- der zweifachen Standardabweichung (das entspräche dem Bereich 160cm bis 200 cm).
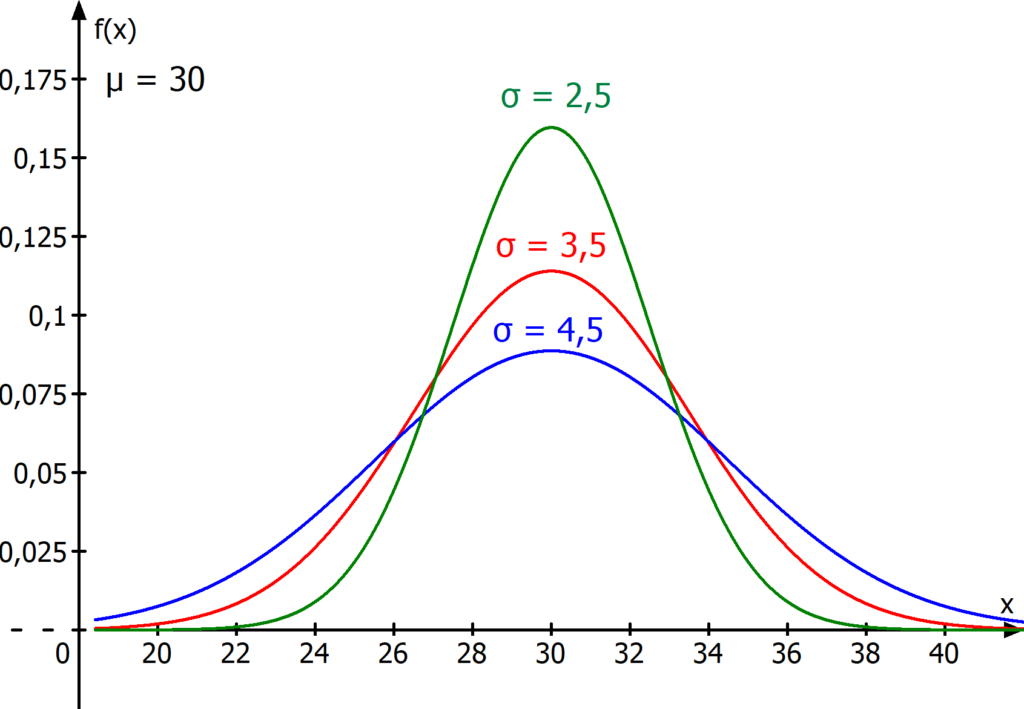
Dichtefunktion Normalverteilung
- besteht aus dem Erwartungswert μ und der Standardabweichung σ
- ist symmetrisch zur Symmetrieachse y= μ
- ist nie 0.
- ist unimodal (eingipflig)
- erreicht ihr Maximum am Erwartungswert μ
- ist bei ihrer Ableitung positiv für Werte von x < µ und negativ für Werte von x > µ
Wie viel sollte man mit 1.90 wiegen
Body-Mass-Index (BMI)
| Gewichtskategorie (BMI) | Normal* (≥ 18,5 und < 25) | Fettleibig: Klasse III (≥ 40) |
|---|---|---|
| 178–180 cm | 60 bis 78 kg | > 127 kg |
| 183–185 cm | 64 bis 83 kg | > 134 kg |
| 188–190 cm | 67–87 kg | > 141 kg |
| 193 cm | 71–89 kg | > 145 kg |
Normalverteilung rechnerisch prüfen
Als Ergebnis bekommst du einen p-Wert. Liegt dieser unter 0,05, dann kannst du von einer statistisch signifikanten Abweichung von der Normalverteilung ausgehen. Ist der Wert größer als 0,05 dann sind deine Daten höchstwahrscheinlich normalverteilt.In diesem Artikel stelle ich Ihnen fünf Wege vor, die Sie in dieser Situation einschlagen können.
- Ausreißer bereinigen. Wenn das eigentliche Problem gar nicht die fehlende.
- Daten transformieren.
- Über Robustheit argumentieren.
- Nicht-parametrische Methoden verwenden.
- Bootstrapping nutzen.
Die Häufigkeiten des Auftretens seltener Krankheiten sowie die Anzahl der Auto- unfälle sind z.B. nicht normalverteilt.
Wann muss ich auf Normalverteilung testen : Normalverteilung rechnerisch prüfen
Als Ergebnis bekommst du einen p-Wert. Liegt dieser unter 0,05, dann kannst du von einer statistisch signifikanten Abweichung von der Normalverteilung ausgehen. Ist der Wert größer als 0,05 dann sind deine Daten höchstwahrscheinlich normalverteilt.
Wie schwer sollte man bei 180 cm sein : Die Einteilung in Normal- und Idealgewicht nach dem Broca-Index gilt als veraltet. Dabei werden von der Größe in Zentimetern 100 abgezogen und ergeben das Normalgewicht. Bei 180 Zentimetern Größe entspräche das 80 Kilogramm. Das Idealgewicht läge um zehn Prozent darunter, in diesem Fall bei 72 Kilogramm.
Wie viel Kilo bei 175 cm
Body-Mass-Index (BMI)
| Gewichtskategorie (BMI) | Normal* (18,5–24) | Übergewicht (25-29) |
|---|---|---|
| 168–170 cm | 54 bis 69 kg | 70–84 kg |
| 173–175 cm | 57–74 kg | 74–89 kg |
| 178–180 cm | 60 bis 78 kg | 79 bis 94 kg |
| 183–185 cm | 64 bis 83 kg | 84–99 kg |

Die abhängige Variable sollte bei einer einfaktoriellen ANOVA für jede Gruppe etwa normalverteilt sein. Ist dies der Fall, so lassen sich die Ergebnisse am fehlerfreisten interpretieren.In der Realität erklärt ein lineare Regressionsmodell nie perfekt alle Beobachtungen. Damit entstehen Abweichungen zwischen den vorhergesagten Werte (in der Grafik oben auf der roten Linie) und den tatsächlichen Werten (in der Grafik die Punkte). Und diese Abweichungen (Residuen) sollten normalverteilt sein.
Wie erkenne ich ob etwas normalverteilt ist : Metrische Messwerte sind dann normalverteilt, wenn ihre Verteilung einer Glockenkurve wie in Abbildung 1 entspricht. Abweichungen von der Normalverteilung lassen sich mit Kennwerten wie Schiefe und Exzess (Wölbung) beschrei- ben. Sind Schiefe und Exzess gleich Null, so liegt perfekte Normalverteilung vor.



