Antwort Hat eine Funktion dritten Grades immer einen Wendepunkt? Weitere Antworten – Hat eine Funktion dritten Grades einen Wendepunkt

Wendepunkte a) Erläutere: Der Funktionsgraph eines Polynoms 3. Grades hat immer genau einen Wendepunkt.Bem.: Lineare Funktionen können keinen Wendepunkt haben, weil ihre Krümmung überall Null ist.Wenn der Wert links von der Stelle positiv ist und rechts davon negativ, dann liegt dort ein Wendepunkt, der von einer Linkskurve zu einer Rechtskurve wechselt. Haben die Werte das gleiche Vorzeichen, dann liegt kein Wendepunkt vor.

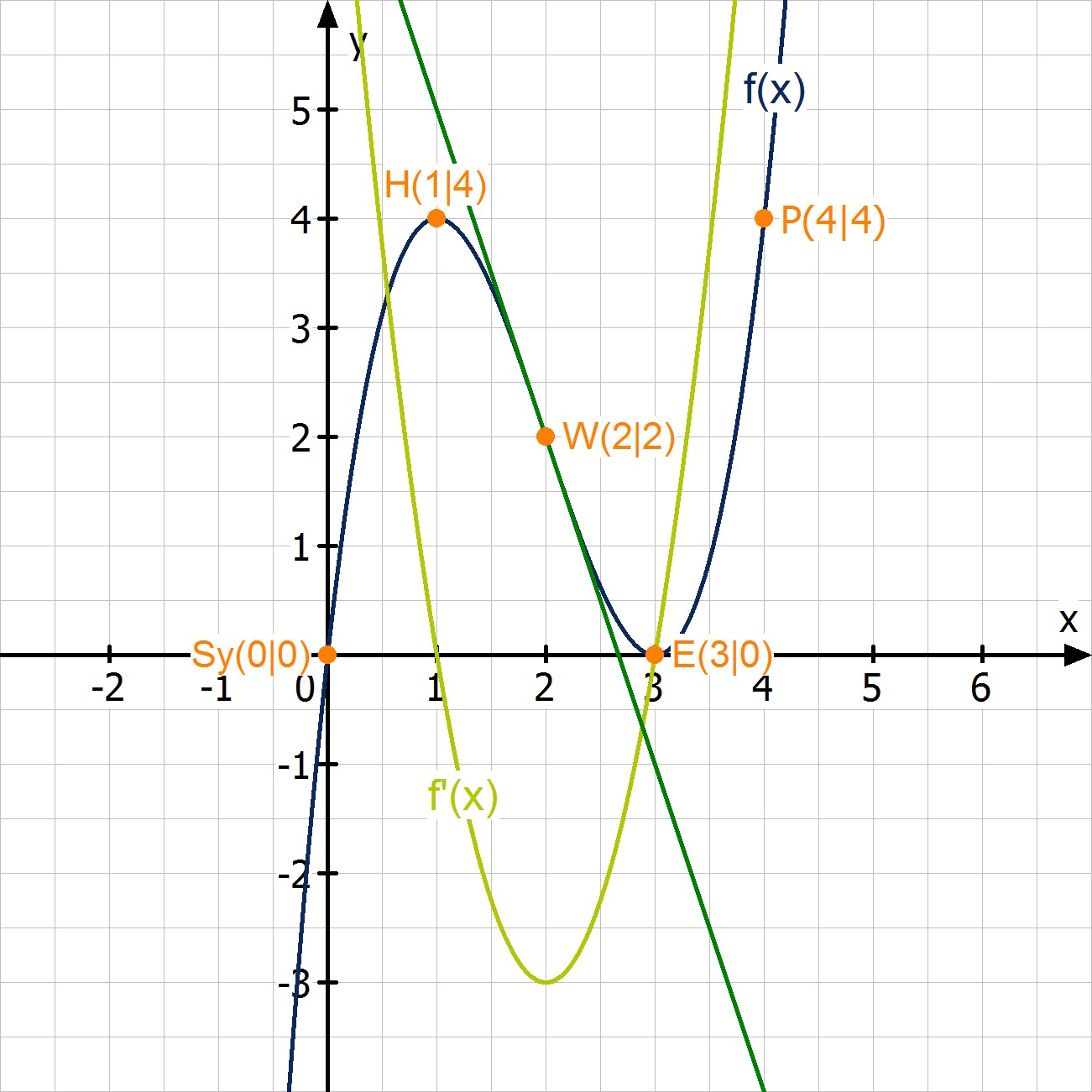
Welche Eigenschaften hat eine Funktion dritten Grades : Funktionen dritten Grades werden auch kubische Funktionen genannt. Diese Funktionen können zwei grundlegende Formen annehmen. Entweder sie besitzen einen Sattelpunkt oder sie besitzen einen Hoch- und einen Tiefpunkt.

Wie viele Wendestellen kann eine Funktion 3 Grades haben

Jede Polynomfunktion dritten Grades hat genau eine Wendestelle. Jede Polynomfunktion dritten Grades hat höchstens zwei lokale Extremstellen.

Hat eine Funktion 4 Grades einen Wendepunkt : Verallgemeinert lässt sich sagen, dass Funktionen mit geradem Exponenten ab 4. Grades Wendepunkte haben können, Funktionen mit ungeradem Exponenten ab 3. Grades mindestens eine Wendestelle haben.

Arten von Wendepunkten

Funktionen 2. Ordnung, also quadratische Funktionen z.B. f(x)=x² können keine Wendepunkte haben, da sich die Krümmung des Graphen nicht ändert.

Eine hinreichende Bedingung für eine Wendestelle ist, dass die zweite Ableitung null wird und die dritte Ableitung an dieser Stelle ungleich null ist. Eine andere hinreichende (und oft leichter zu überprüfende) Bedingung hierfür ist, dass die zweite Ableitung verschwindet und an dieser Stelle ihr Vorzeichen wechselt.

Wie viele Wendepunkte kann eine Funktion 3 Grades haben

Jede Polynomfunktion dritten Grades hat genau eine Wendestelle. Jede Polynomfunktion dritten Grades hat mehr Null- stellen als lokale Extremstellen. Jede Polynomfunktion dritten Grades hat mindestens eine lokale Maximumstelle. Jede Polynomfunktion dritten Grades hat höchstens zwei lokale Extremstellen.Eine Polynomfunktion hat maximal so viele Nullstellen, wie ihr höchster Grad! Eine Funktion dritten Grades kann also höchstens 3 Nullstellen haben!Eine Polynomfunktion hat maximal so viele Nullstellen, wie ihr höchster Grad! Eine Funktion dritten Grades kann also höchstens 3 Nullstellen haben!

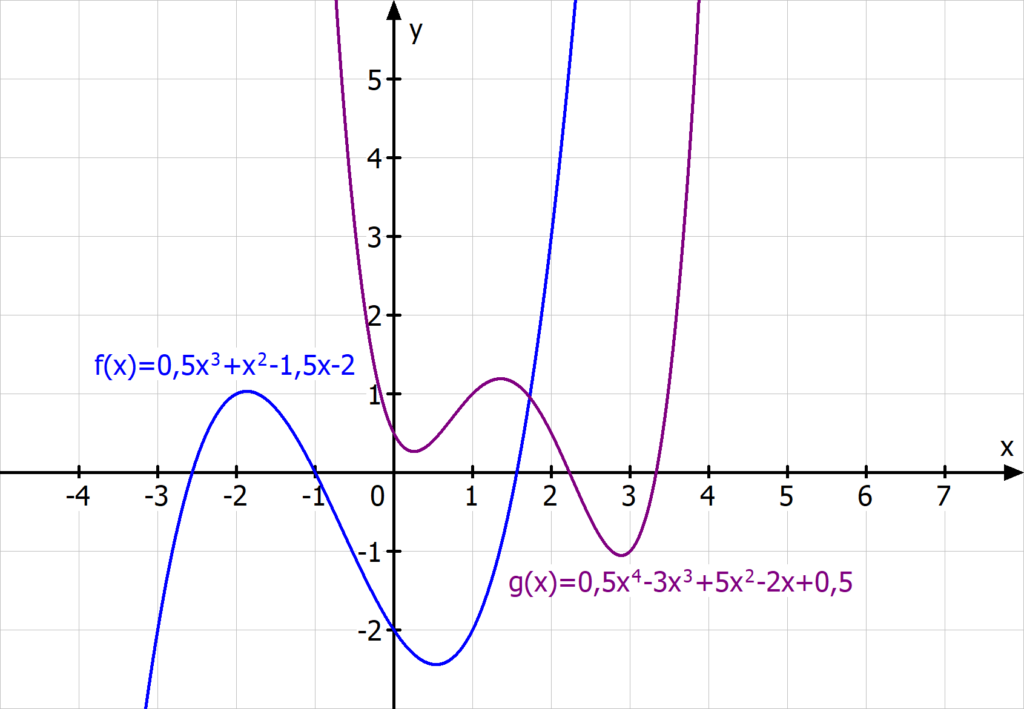
Funktionen 2. Ordnung, also quadratische Funktionen z.B. f(x)=x² können keine Wendepunkte haben, da sich die Krümmung des Graphen nicht ändert. Funktionen 3. Ordnung, also kubische Funktionen haben immer einen Wendepunkt.

Wann hat eine Funktion eine Wendestelle : Ein Punkt P(x0|f(x0)) des Graphen Gf einer Funktion f heißt Wendepunkt (und die Stelle x0 dann eine Wendestelle), wenn sich dort die Krümmung des Graphen ändert. Die Tangente an diesem Punkt ist die Wendetangente. Ein Wendepunkt mit waagerechter Tangente ist ein Sattelpunkt bzw. Terrassenpunkt.

Wie viele Wendepunkte kann eine Funktion 4 Grades haben : Jede Polynomfunktion, deren Grad größer als 3 ist, hat mindestens eine lokale Extremstelle. Jede Polynomfunktion dritten Grades hat genau eine Wendestelle. Jede Polynomfunktion vierten Grades hat mindestens eine Nullstelle.

Wie viele Wendepunkte hat eine Funktion 2 Grades

Funktionen 2. Ordnung, also quadratische Funktionen z.B. f(x)=x² können keine Wendepunkte haben, da sich die Krümmung des Graphen nicht ändert. Funktionen 3. Ordnung, also kubische Funktionen haben immer einen Wendepunkt.

Eine Polynomfunktion hat maximal so viele Nullstellen, wie ihr höchster Grad! Eine Funktion dritten Grades kann also höchstens 3 Nullstellen haben!Eine ganzrationale Funktion 3. Grades wird kubische Funktion genannt. Hier lassen sich die wichtigsten Punkte wie folgt zusammenfassen: allgemeine Funktionsgleichung: f(x)=a3x3+a2x2+a1x+a.

Kann eine Funktion 4 Grades keine Nullstelle haben : Jede Polynomfunktion vierten Grades hat mindestens eine Nullstelle.