Antwort Für was braucht man den Cosinus? Weitere Antworten – Für was braucht man den Kosinussatz
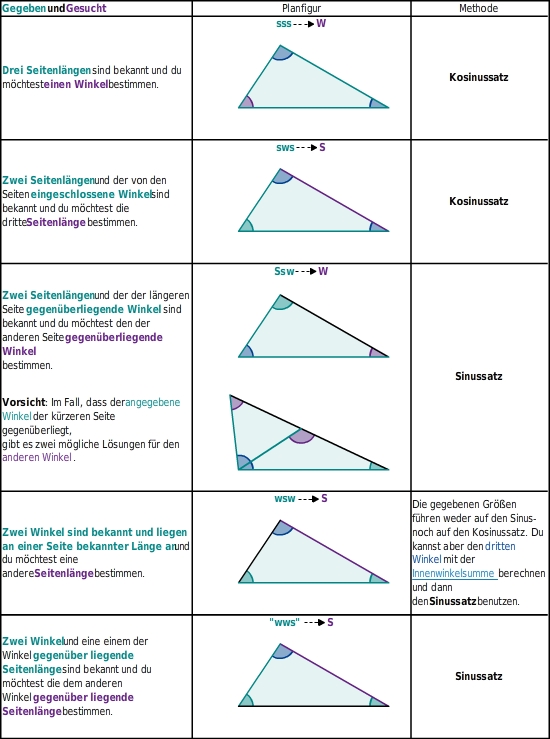
Du kannst den Kosinussatz anwenden, wenn:
- zwei Seiten und der eingeschlossene Winkel gegeben sind und Du die dem Winkel gegenüberliegende Seite berechnen möchtest.
- alle drei Seiten des Dreiecks gegeben sind und Du einen Winkel berechnen möchtest.
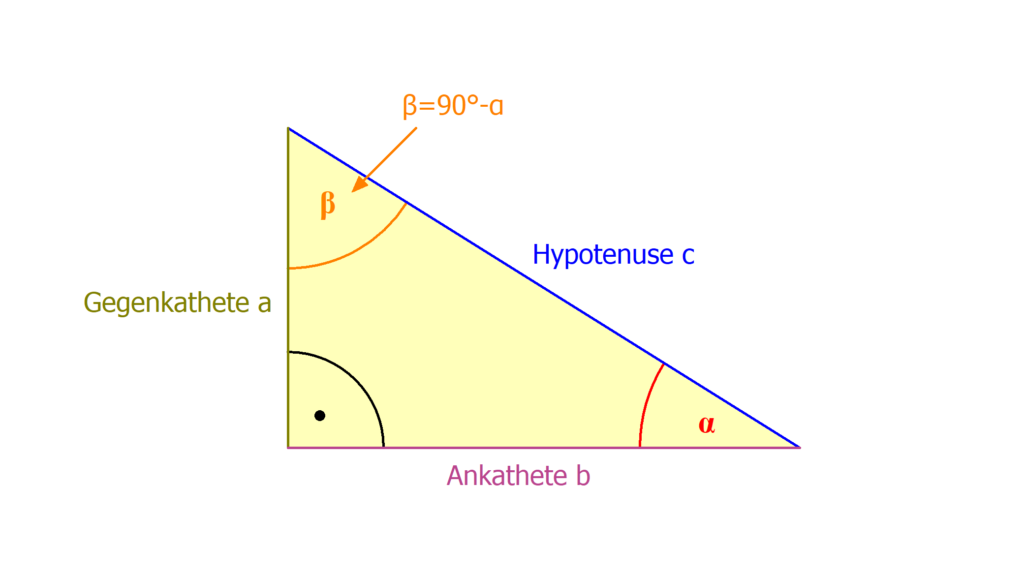
Mit dem Cosinus kannst du fehlende Winkel oder Seiten in einem rechtwinkligen Dreieck bestimmen. Dabei ist der Cosinus das Verhältnis zweier Seiten: der Ankathete und Hypotenuse des Dreiecks. Mit einem geometrischen Trick kannst du die Definition auf den Einheitskreis erweitern.Der Kosinus ist das Verhältnis der Länge der Ankathete (das ist jene Kathete, die einen Schenkel des Winkels bildet) zur Länge der Hypotenuse. Auf dieser Beziehung beruht auch die Bezeichnung Kosinus als Sinus des Komplementärwinkels. -Koordinate eines Punktes am Einheitskreis (siehe unten) definiert.
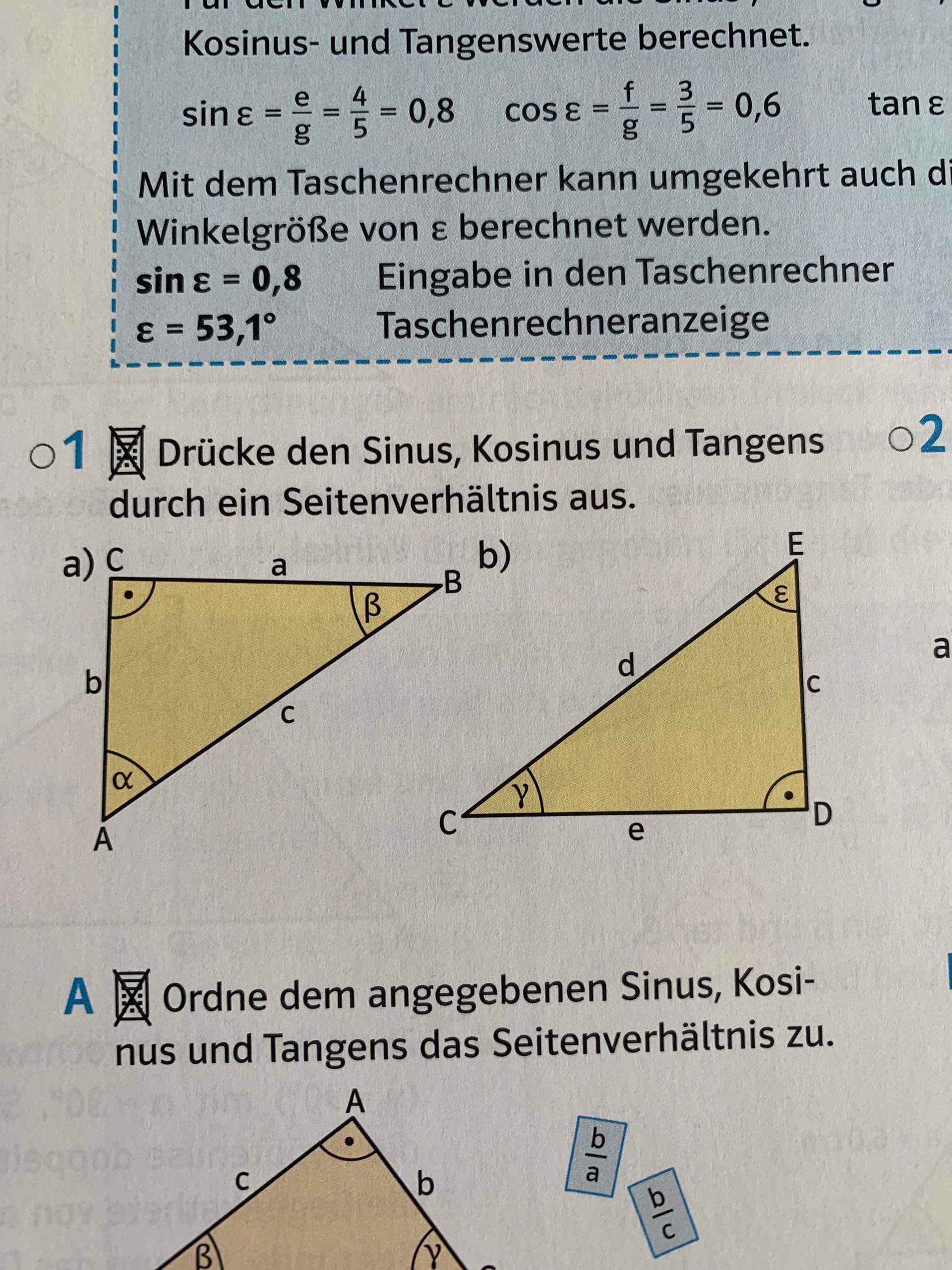
Wo braucht man Sinus : Die Winkelfunktionen Sinus, Kosinus und Tangens verwendest du, wenn du die Länge einer Seite oder die Größe eines Winkels in einem rechtwinkligen Dreieck berechnen möchtest.
Für was braucht man Sinus Kosinus und Tangens
Der Sinus, der Cosinus und der Tangens werden angewendet, um Winkel und Seiten rechtwinkliger Dreiecke zu bestimmen.
Wann würden Sie die Kosinusregel anwenden : Um ein Dreieck zu lösen, müssen die Längen jeder seiner Seiten und alle seine Winkel ermittelt werden. Die Sinusregel wird verwendet, wenn uns entweder a) zwei Winkel und eine Seite oder b) zwei Seiten und ein nicht eingeschlossener Winkel gegeben sind. Die Kosinusregel wird verwendet , wenn uns entweder a) drei Seiten oder b) zwei Seiten und der eingeschlossene Winkel gegeben sind .
Die Kosinusfunktion ordnet jedem Winkel eine Streckenlänge zu. Die Länge der blau gezeichneten Strecke gehört dabei zu dem Winkel x. Ist x zum Beispiel mit 60° gegeben, so ist die Länge der blauen Strecke 0,5. Daher ist cos 60°=0,5.
Kosinusfunktion – Das Wichtigste
Die Kosinusfunktion hat einen Wertebereich W f von W f = [ – 1 , 1 ] . Aus dem Wertebereich ergibt sich eine Amplitude a = 1 . Die Kosinusfunktion weist eine Achsensymmetrie zur y – Achse auf. Der y – Achsenabschnitt der Kosinusfunktion ist y = 1 .
Wann benutzt man Sinus oder Cosinus
Der Sinus eines Winkels ist definiert als das Verhältnis der Länge der Gegenkathete zur Länge der Hypotenuse. Der Cosinus eines Winkels ist definiert als das Verhältnis der Länge der Ankathete zur Länge der Hypotenuse.Der Sinus ist eine wichtige trigonometrische Funktion, mit welcher du zum einen Winkel in einem rechtwinkligen Dreieck berechnen kannst und zum anderen ist er sehr nützlich, um periodische Vorgänge in der Physik zu beschreiben, wie zum Beispiel Wellen.Der Tangens als Quotient aus Sinus und Kosinus.
Sinus und Kosinus – auch bekannt als sin(θ) und cos(θ) – sind Funktionen, die die Form eines rechtwinkligen Dreiecks offenbaren. Von einem Scheitelpunkt mit dem Winkel θ aus gesehen ist sin(θ) das Verhältnis der gegenüberliegenden Seite zur Hypotenuse, während cos(θ) das Verhältnis der benachbarten Seite zur Hypotenuse ist .
Woher wissen Sie, wann Sie sin oder cos verwenden sollten : Wenn das Gegenteil und die Hypotenuse verwendet werden, verwenden Sie für die Berechnungen den Sinus. Wenn Ankathete und Hypotenuse verwendet werden, verwenden Sie den Kosinus . Wenn das Gegenteil und das Angrenzende verwendet werden, verwenden Sie Tangente. Sie können sich dies mit dem Akronym SOH CAH TOA merken.
Wie lautet die einfache Kosinusformel : Mit anderen Worten, der Kosinus eines Winkels in einem rechtwinkligen Dreieck entspricht der Ankathete dividiert durch die Hypotenuse: Außerdem gilt: cos A = sin B = b/c .
In welcher Klasse lernt man Sinus und Cosinus
In Jahrgangsstufe 10 erweitern die Schüler die Definition von Sinus und Kosinus auf beliebige Winkel; dabei werden neben geometrischen ausdrücklich auch funktionale Aspekte der Trigonometrie vom Lehrplan eingefordert.
Der Tangens als Quotient aus Sinus und Kosinus.Sinus, Kosinus und Tangens können zur Lösung fehlender Seiten verwendet werden, wenn mindestens eine Seite und ein spitzer Winkel in einem rechtwinkligen Dreieck bekannt sind . Die verwendete Funktion wird durch die gegebenen Informationen bestimmt.
Wie hängen Sinus und Cosinus zusammen : Die Winkelfunktionen Sinus und Cosinus repräsentieren dabei das Verhältnis von Kathete zu Hypotenuse. Trigonometrische Funktionen: sin (Winkel) = Gegenkathete : Hypotenuse. cos (Winkel) = Ankathete : Hypotenuse.